EWC14 – Match Two: Catenaccio & Ecological Niche Theory.

In football, like science, competing paradigms and co-existing concepts are common. Despite the revolutionary ideas and performances of Sebes and Puskás, other tactical systems flourished in the 1950s and 1960s. The Catenaccio (literally meaning door-bolt in Italian) is a tactical system in football which implies a highly organized, structured and competitive backline defence. The tactic focuses on protecting space to minimise goal-scoring opportunities. Making a team defensively compact, while trying to score goals at the other end.

Italy using Catenaccio to stop Spain.

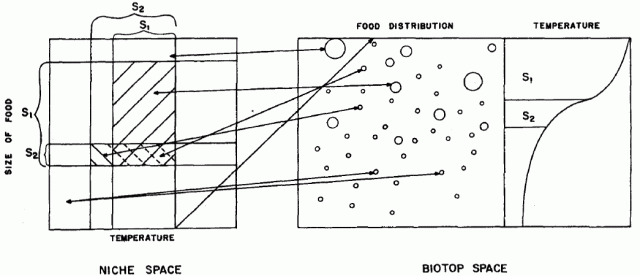
Parallels can be drawn between the Catenaccio system and Ecological Niche theory. Niche theory was formally defined in 1957, when G. Evelyn Hutchinson defined a niche as an n-dimensional hyper-volume. Where the dimensions are environmental conditions and the resources that define the requirements of an individual or a species.

If we think of a football team as species and a player as an individual, we can start to conceptualise niche in practice. Without a competing team (inter-specific competition), a football team is free to pass the ball and have shots at goal. Really, they are just limited by their own abilities and the confines of a football pitch. This is the Fundamental Niche. However, in a match situation opposing teams (species) and players (individuals) are interacting. They compete for the ball and space. Forcing teams to occupy a smaller space than they would occupy without competition. This is called the Realised Niche.

Two fundamental niches defined by a pair of variables in a two-dimensional niche space. As depicted in Hutchinsons 1957 paper.

Two fundamental niches as depicted in Hutchinson’s 1957 paper.

Catennacio like Niche theory has had plenty of success, for football the Italian club teams of the 60, 70s and 90s and the national team all had success using this tactic, most recently in 2006 where they used an updated version to claim the 2006 world cup final. In ecology, niche theory is alive and well and still remains widely implemented and debated in fields such species distribution modelling and community ecology.

There is a long history in the ecological literature that aims to understand what processes drive interactions between species. One of the most famous in the Lotka-Volterra competition model. The Lotka–Volterra model is a pair of differential equations, used to describe the dynamics of biological systems in which two species interact. If we want explicitly explore this concept, we can think of the famous Lotka-Volterra model in terms of football.

The following equations represent a model of continuous logistic competition between two species. For the purposes of our soccer analogy the equations represent the success of two competing teams.

$\Large \frac{d N_{1}}{d t} = r_{1}N_{1}(1-\alpha_{11}N_{1}-\alpha_{12}N_{2})$
$\Large \frac{d N_{2}}{d t} = r_{2}N_{2}(1-\alpha_{21}N_{2}-\alpha_{21}N_{2})$

$r_{i}$ Represents individuals produced per individual per unit time. As we are thinking of this in terms of football, this might be the appearance of new players? However as that doesn’t really make sense in terms of a football match, let’s think of this as number of passes achieved at each time step. A proxy for a teams competitive edge.

$\alpha_{ii}$ Is the effect of intra-specific competition between individuals of species i on the overall population size. Once again in terms of football this might represent the tempo as game is played at? If the tempo (speed a team plays) is fast, you might expect to out play the opposition. If you play really fast then we might expect teams to get tired, their passing starts to fall apart and eventually you lose due to exhaustion. Additionally, if a team’s tempo is too slow and you lose (Unless you’re the Spanish team, as we’ll discover in the example below).

$\alpha_{ij}$ Is the negative effect of inter-specific competition of species j has on the growth rate of species i or vice versa. For the purposes of my football example, we are going to think of this as pressure from the opposing team.

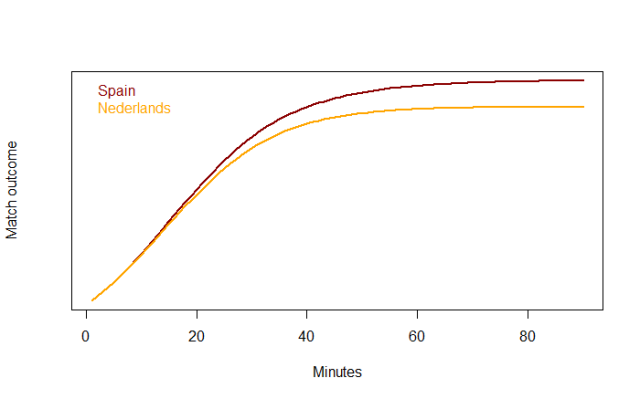
Now it pains me to revisit the 2010 Football World Cup because of my Dutch heritage. But for the sake of science, I’ll use the 2010 WC final as an example of this model applied to football. And as we know the result (Spain won), I have fixed the match to enable Spain to win. As you can see in the example figure below.

A Lotka-Volterra model that depicts the outcome of the 2010 EWC final.

Now if you want to see what are the effects of $\alpha_{ii}$ and $\alpha_{ij}$ on the outcomes of our 2010 EWC final you can visit this Shiny app I’ve created to see what happens. What happens if you increase the tempo ( $\alpha_{ii}$ ) and pressure ( $\alpha_{ij}$ ) Spain exert on the Dutch team? What happens if the Spanish team drank to much Sangria and play terribly? Have a play and see if you can alter the outcome of 2010 Ecological World Cup.

Well that’s it for another week of Ecological World Cup 14. Next week I might try and explore the links between Total Football and Neutral Theory.

And as Alan Partridge would say: “That was liquid football.”

1 Response to EWC14 – Match Two: Catenaccio & Ecological Niche Theory.

Pingback: Dbytes #153 (17 June 2014) | Dbytes